扩散模型的基本原理与公式推导

扩散模型(Diffusion Model)

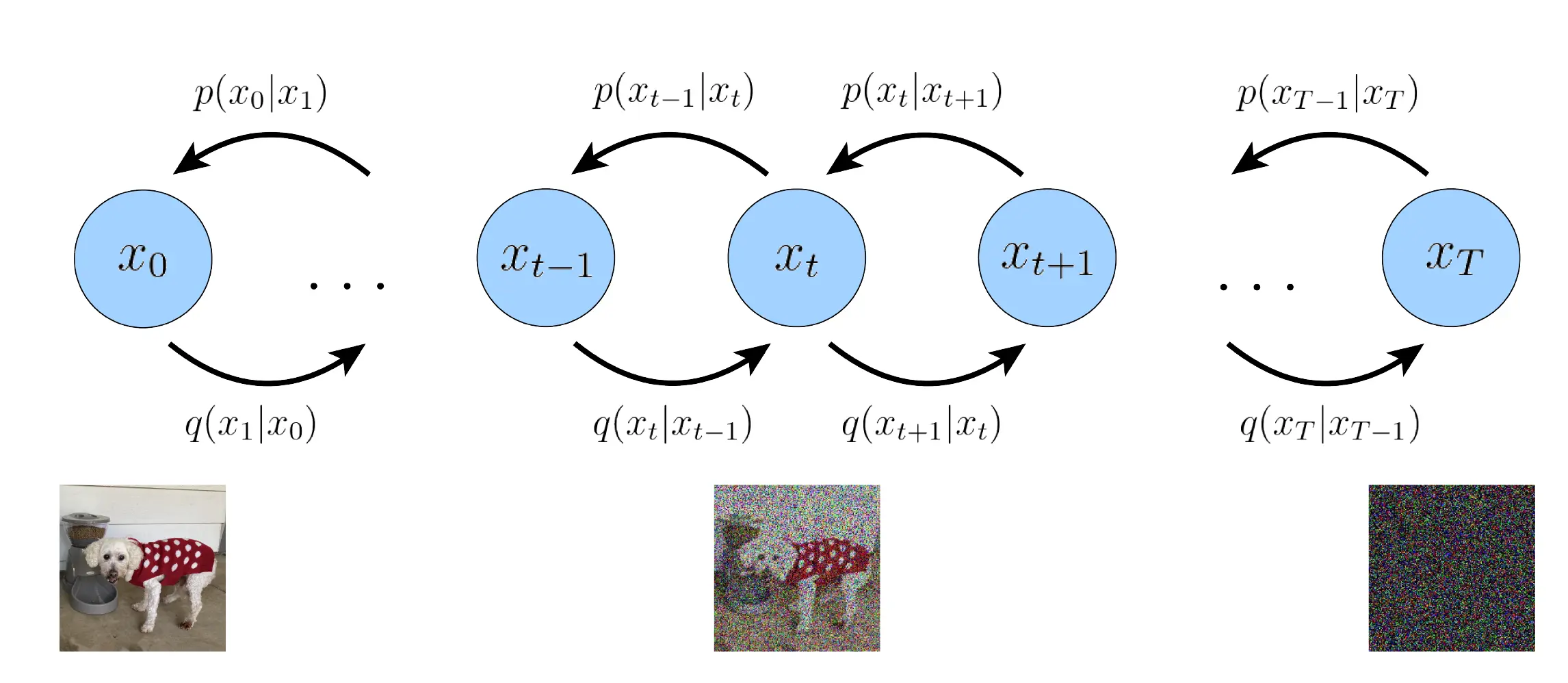
通过连续添加高斯噪声来破坏训练数据，然后通过反转这个噪声过程，来学习恢复数据。主要包括以下两个过程，

• 正向扩散过程 $q$: 逐渐将高斯噪声添加到图像中，直到最终得到纯噪声；
• 逆向去噪过程 $p_{\theta}$: 通过训练神经网络从纯噪声开始逐渐对图像去噪，直到最终得到一个实际的图像。

前向过程(扩散过程)

条件概率分布

通过在 $T$ 个有限时间步内不断对图像添加高斯噪声
设最初的图像样本 $x_0$，对应的真实数据分布为 $x_0\sim q(x_0)$，并且控制每个时间步对应的缩放因子有如下关系：
$$0<\beta_1<\beta_2<\cdots<\beta_T=1\tag{1}$$
给定样本的前一步状态$x_{t-1}$，可以得到当前状态$x_t$的条件概率分布:
$$q(x_t|x_{t-1}) = N(x_t;\sqrt{1-\beta_t}x_{t-1}, \beta_t I)\tag{2}$$
其中，$N(\mu, \sum)$表示多维正态分布，均值为$\mu$，协方差矩阵为$\sum$，提取的样本特征$x$为多维变量，因此表示为多维正态分布。直接的含义解释，设定缩放因子$\beta_t$缩放前一步的样本特征$x_{t-1}$，并在样本特征的多个维度上添加独立同分布的噪声（单位矩阵）。

扩散过程可以表示为：
$$q(x_{1:T}|x_0) = \prod_{t=1}^T q(x_t|x_{t-1})\tag{3}$$

Theory 1 重参数 (Reparameterization Trick)
多维随机变量 $z$ 服从分布 $z\sim N(z;\mu_{\theta}, \sigma_{\theta}^2 I)$，则可以将其进一步表示为
$$z=\mu_{\theta} + \sigma_{\theta} \cdot \epsilon, \epsilon \sim N(0, I)\tag{4}$$

$z$ 的随机性转移为 $\epsilon$ 的随机性。

概率分布推导

Supposing $x_0\sim N(x_0;\mu_0, \sigma_0^2 I)$, then
$$x_t = \sqrt{1-\beta_t}x_{t-1} + \beta_t \epsilon_{t-1}\tag{5}$$
令 $\alpha_t = 1-\beta_t$, then
$$\begin{aligned} x_t &= \sqrt{\alpha_t} x_{t-1} + \sqrt{1-\alpha_t}\epsilon_{t-1} \newline x_{t-1} &= \sqrt{\alpha_{t-1}} x_{t-2} + \sqrt{1-\alpha_{t-1}}\epsilon_{t-2} \end{aligned}\tag{6}$$
故
$$\begin{aligned} x_t &= \sqrt{\alpha_t}(\sqrt{\alpha_{t-1}}x_{t-2} + \sqrt{1-\alpha_{t-1}}\epsilon_{t-2})+\sqrt{1-\alpha_t}\epsilon_{t-1}\newline &= \sqrt{\alpha_{t-1}\alpha_t} x_{t-2} + \sqrt{\alpha_t}\sqrt{1-\alpha_{t-1}}\epsilon_{t-2}+\sqrt{1-\alpha_t}\epsilon_{t-1} \end{aligned}\tag{7}$$
For $\sqrt{\alpha_t}\sqrt{1-\alpha_{t-1}}\epsilon_{t-2}$ 可表示为
$$z_1 = 0 + \sqrt{\alpha_t}\sqrt{1-\alpha_{t-1}}\epsilon_{t-2}\sim N(0, \alpha_t(1-\alpha_{t-1}) I)\tag{8}$$
For $\sqrt{1-\alpha_{t}}\epsilon_{t-1}$ 可表示为
$$z_2 = 0 + \sqrt{1-\alpha_t}\epsilon_{t-1}\sim N(0, (1-\alpha_t) I)\tag{9}$$
Theory 2 两个正态随机变量和 $z =z_1+z_2$
Conditions: $z_1 \sim N(\mu_1, \sigma^2_1), z_2 \sim N(\mu_2, \sigma^2_2), Cov(z_1, z_2) = 0$
Conclusions:
$$EZ = EZ_1 + EZ_2 = \mu_1 + \mu_2\newline DZ = DZ_1 + DZ_2 + 2Cov(z_1, z_2) = \sigma^2_1 + \sigma^2_2\tag{10}$$
记 $z=z_1+z_2\sim N(0, (1-\alpha_t\alpha_{t-1})I)$，则可得
$$\begin{aligned} x_t &= \sqrt{\alpha_{t-1}\alpha_t}x_{t-2} + \sqrt{1-\alpha_t\alpha_{t-1}}\epsilon_{t-2}\newline &=\cdots\newline &=\sqrt{\alpha_t\alpha_{t-1}\cdots\alpha_1}x_0 + \sqrt{1-\alpha_t\alpha_{t-1}\cdots\alpha_1}\epsilon_0\newline &=\sqrt{\overline{\alpha_t}}x_0 + \sqrt{1-\overline{\alpha_t}}\epsilon \end{aligned}\tag{11}$$
其中，$\overline{\alpha_t} = \prod_{i=1}^t\alpha_i$.
进一步结合公式 (2)，可以得到在初始状态条件下的第 $t$ 步的概率分布
$$q(x_t|x_0) =N(x_t; \sqrt{\overline{\alpha_t}}x_0, \sqrt{1-\overline{\alpha_t}}I)\tag{12}$$
Analysis of $\beta_i$:
已知 $0 < \beta_1 < \beta_2 < \cdots < \beta_T = 1$，则
$$1 > \alpha_1 > \alpha_2 > \cdots > \alpha_T > 0\tag{13}$$
当 $\alpha$ 满足收敛性时，$\exists T > 0, \epsilon > 0$, 当 $t > T$ 时, $|\overline{\alpha_t} - 0| < \epsilon$, 则
$$\begin{aligned} x_t &= \sqrt{\overline{\alpha_t}}x_0 + \sqrt{1-\overline{\alpha_t}}\epsilon\newline &\sim N(\sqrt{\overline{\alpha_t}}x_0, (1-\overline{\alpha_t}) I)\newline &\overset{t>T}{\longrightarrow} N(0, 1) \end{aligned}\tag{14}$$

反向过程(逆扩散过程)

$$p(x_0|x_{1:T}) = \frac{1}{Z} \exp(-\beta_t \cdot \frac{1}{2} \cdot (x_t - \sqrt{1-\beta_t}|x_{t-1})^2)$$